CS 10C Programming Concepts and Methodologies 2

Section 20.1: Introduction to Linked Lists

You'll notice that the approach to implementing nodes taken here is different from the textbook's approach. In the textbook a "Node" class that is separate from the main class is introduced, with accessors and mutators to use when you need to access the elements in the class. In the lesson, I simply declare a "node" struct inside the main class. I think it will be instructive to see both approaches.

To a large extent, what we will be doing from now on will be studying a variety of ADT's. We'll be focusing primarily on how those ADT's are implemented. This might feel a little frustrating to some of you. It's a little like studying how to build an engine when what you really want to do is race the car. In this class you'll be doing a little racing, but the philosophy is that learning how to build an engine is the best way to learn how to race most effectively. Personally I love this stuff simply because it is fun to work on the engine. For some of you who prefer to get on with the racing, you will have to exercise some patience.

Until now we have had only one way of storing a lot of data in a variable: arrays. True, we can use vectors, but a vector is really just an array when you look behind the scenes. Now we're going to study something completely new: linked lists. The STL container class that is implemented using the type of linked list we'll be studying is called forward_list.

Unlike the data stored in an array, the data stored in a linked list is not stored in contiguous memory locations. The first piece of data is stored in some memory location, along with a pointer to the second piece of data, which may be stored at a memory location someplace nowhere near the first piece of data. Each piece of data in the list is stored along with a pointer to the following piece of data. Here's a picture of a linked list that has three elements:

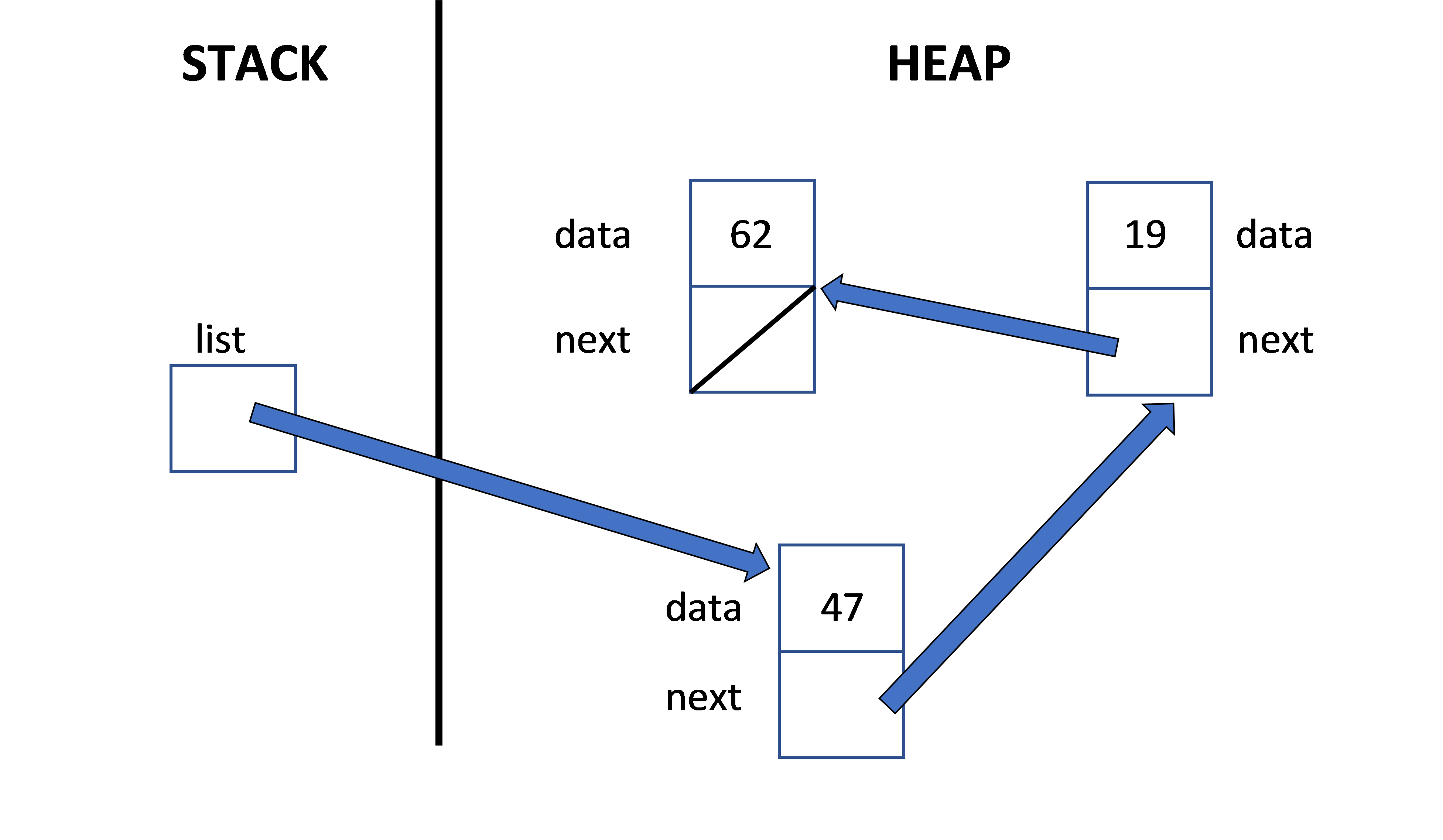
Each of those boxes in the linked list is called a node. When we are at the end of the list, there is no "next" item, so the pointer is nullptr. (Recall that we represent nullptr in our diagrams by drawing a diagonal line through the box.)

Section 20.2: The SimpleList Class

Ok, let's go back to working on the details of implementing a linked list. We're going to start with a very simple, streamlined class that will store integers in a linked list. Because we want to start simple, this one won't be much like the STL forward_list. In fact, let's call it "SimpleList". Here's a client program to get us started.

#include <iostream>
#include "simplelist.h"
using namespace std;
using namespace harden_list;


int main() {
    SimpleList myList;

    int num;

    cout << "enter number to insert (negative to quit): ";
    cin >> num;
    while (num >= 0){
        myList.insert(num);
        cout << "enter number to insert (negative to quit): ";
        cin >> num;
    }

    myList.print();
    cout << endl;
}

Looking at this client program, you can see that we'll need three member functions: insert(), print(), and a constructor.

We'll also need a data member named list that points to the first node in the linked list, and we'll also need to declare a new type named node. A node will have two data members: one to store the data, named data, and one to store a pointer to the next node in the linked list, named next.

How will we create this new type? Will it be a class? A struct? Where should we declare it? Our approach will be to create a struct named "node" inside the SimpleList class. Because we'll be declaring it in the private area of our SimpleList class, other classes won't have access to it, but member functions of the SimpleList class will be able to access the node's data freely.

Here's the class declaration I have described so far:

// Here is the file simplelist.h

#ifndef SIMPLELIST_H
#define SIMPLELIST_H

namespace harden_list {
    class SimpleList {
        public:
            SimpleList();
            void insert(const int& insertMe);
            void print() const;
        private:
            struct node {
                int data;
                node* next;
            };
            node* list;
    };
}
#endif

Section 20.3: The SimpleList Class: constructor

For now we will have only a default constructor that will create an empty SimpleList. How will we represent an empty SimpleList? It will be a linked list with no nodes in it, which means that the list data member will be nullptr. Here's the function definition:

    SimpleList::SimpleList() {
        list = nullptr;
    }

Here's what an empty SimpleList looks like:

Section 20.4: The SimpleList Class: insert()

How will we insert an item into a linked list? Our SimpleList class doesn't care where in the list new items are inserted, so we get to choose. Will it be easier (and more efficient) to insert new items at the front of the list, or at the end of the list? It turns out that there is no easy (or efficient) way to insert at the end of our linked list. We would have to start at the front of the list and move down the items one at a time until we reach the last node in the list, and then do our inserting. Much easier (and more efficient) to simply insert at the front of the list. It will take us four steps:

1. Create a new node

   void SimpleList::insert(const int& insertMe) {
       node* newnode = new node;
   }

   

2. Put the data that we are inserting into the new node

   void SimpleList::insert(const int& insertMe) {
       node* newnode = new node;
       newnode -> data = insertMe;
   }

   

3. Make the "next" pointer of the new node point to the node that "list" is currently pointing at.

   void SimpleList::insert(const int& insertMe) {
       node* newnode = new node;
       newnode -> data = insertMe;
       newnode -> next = list;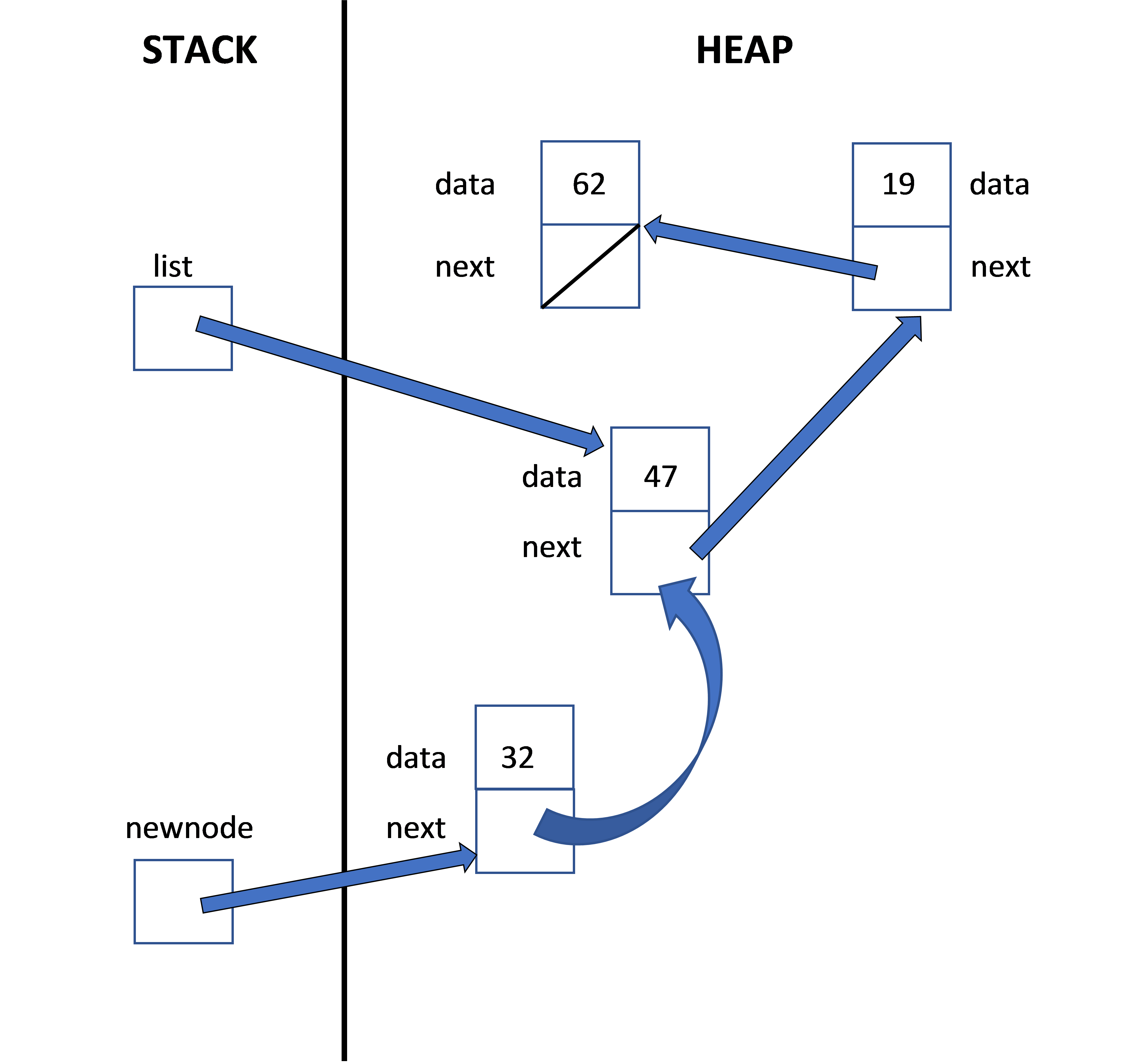
   }

   

4. Make "list" point to the new node.

   void SimpleList::insert(const int& insertMe) {
       node* newnode = new node;
       newnode -> data = insertMe;
       newnode -> next = list;
       list = newnode;
   }

   

Section 20.5: The SimpleList Class: print()

First let me point out that container classes do not usually provide a print() function. This operation is left to the client to implement. However, we will provide one here for more practice with linked list manipulations, and to make it easier to test our class.

Here are the steps for printing a SimpleList.

1. Create a pointer named curptr and make it point to the first node in the linked list

   void SimpleList::print() const {
       node* curptr = list;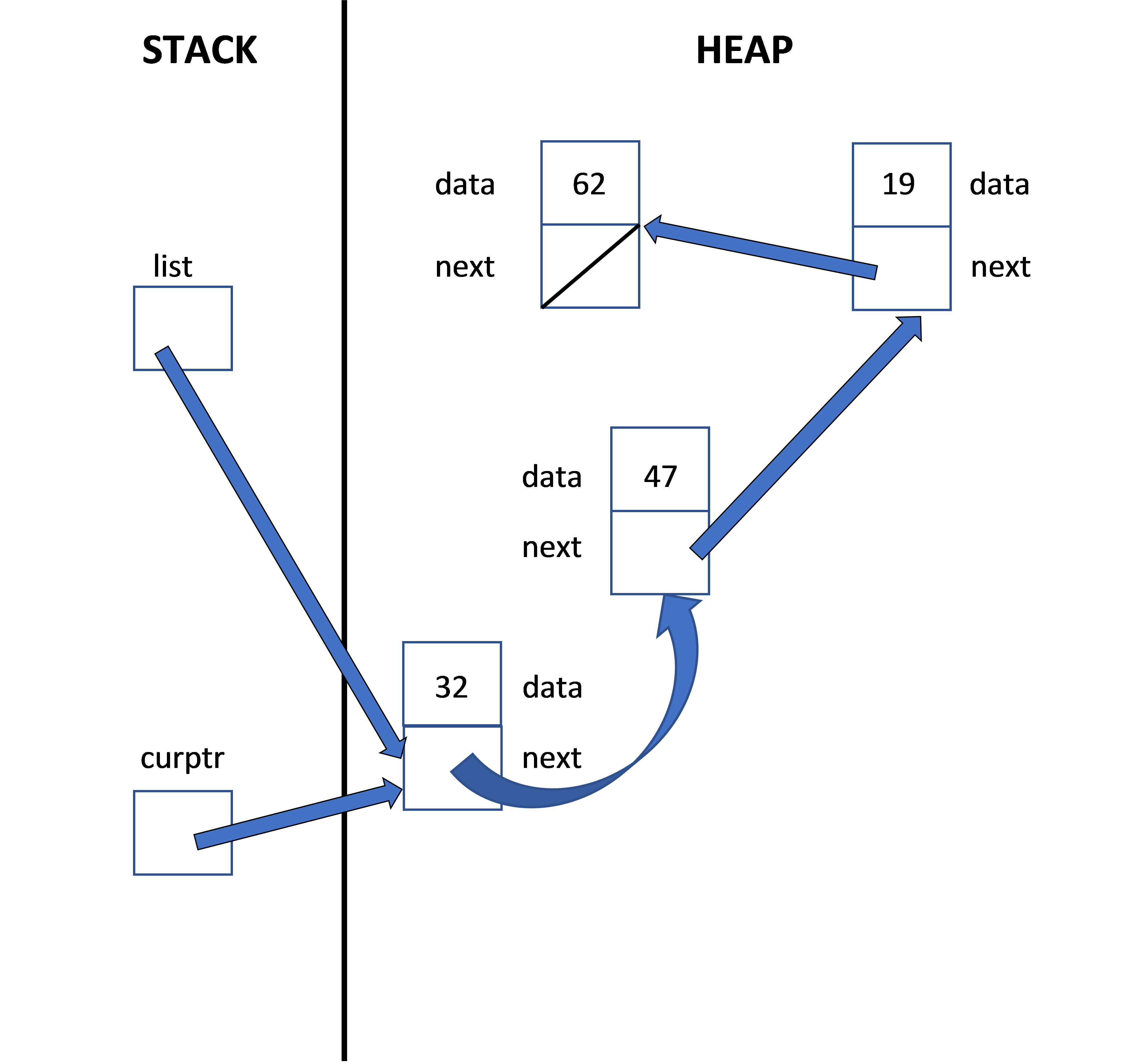
   }
   

   

2. As long as curptr is not nullptr
   1. Print the node that curptr is pointing at
   2. Advance curptr to the next node in the linked list

   void SimpleList::print() const {
       node* curptr = list;
       while (curptr != nullptr) {
           cout << curptr -> data << " ";
           curptr = curptr -> next;
       }
   }
   

Don't read on until you have traced through the print() function to make sure that you understand how it works.

Section 20.6: The Complete SimpleList Code

I'm providing the rest of the SimpleList class in its completed form. The text also does a very good job of explaining linked lists. My suggestion is that you read carefully through the chapter in the text, making sure that you understand every line of code listed. (There is a lot of code in this chapter!) Then study the examples I've provided below. You'll see a lot in common with what you read in the text.

If you can take the time to watch the videos this week, you'll be in even better shape.

Here's our client program to test the class we are going to write. Make sure you study it carefully so you understand what it is that we need our class to do. I suggest you make a list of every public member of the class that we are going to need based just on looking at this client, before moving on to the header file.

// This is the file client.cpp


#include <iostream>
#include "simplelist.h"
using namespace std;
using namespace harden_list;


int main() {
    SimpleList list;

    int num;
    bool found;

    cout << "enter number to insert (negative to quit): ";
    cin >> num;
    while (num >= 0){
        list.insert(num);
        cout << "enter number to insert (negative to quit): ";
        cin >> num;
    }

    list.print();
    cout << endl;

    SimpleList::size_type numItems;
    numItems = list.size();
    cout << "There are " << numItems << " items." << endl;
    cout << "enter a number to find (negative to quit): ";
    cin >> num;
    while (num >= 0) {
        int result = list.find(num, found);
        if (!found) {
            cout << "not found" << endl;
        } else {
            cout << "found.  The data is " << result << endl;
        }
        cout << "enter a number to find (negative to quit): ";
        cin >> num;
    }


    cout << "enter a number to delete (negative to quit): ";
    cin >> num;
    while (num >= 0) {
        list.del(num, found);
        if (found) {
            cout << "the list is now ";
            list.print();
            cout << endl;
        } else {
            cout << num << " is not in the list." << endl;
        }
        cout << "enter a number to delete (negative to quit): ";
        cin >> num;
    }

    SimpleList list2(list);

    cout << "Now list 2 should be a copy of list.  Here it is: ";
    list2.print();
    cout << endl;
    

    list2.del(3, found);


    cout << "After deleting a 3 from list2, list2 is now: ";
    list2.print();
    cout << endl << "list should be unchanged.  Here it is: ";
    list.print();
    cout << endl;

    list = list2;

    cout << "Now list has been assigned list2 so it should match list2.  Here it is: ";
    list.print();
    cout << endl;
    
    list.del(4, found);

    cout << "After deleting a 4 from list, list is now: ";
    list.print();
    cout << endl << "list2 should be unchanged.  Here it is: ";
    list2.print();
    cout << endl;

}

Now the header file, followed by the implementation file

// Here is the file simplelist.h

#ifndef SIMPLELIST_H
#define SIMPLELIST_H
#include <cstdlib>

namespace harden_list {
    class SimpleList {
        public:
            typedef std::size_t size_type;
            typedef int value_type;
            SimpleList();
            void insert(const value_type& insertMe);
            void print() const;
            size_type size() const;
            value_type find(const value_type& findMe, bool& found) const;
            void del(const value_type& deleteMe, bool& found);
            void clear();
            void clone(const SimpleList& cloneMe);
            SimpleList(const SimpleList& copyMe);
            SimpleList operator=(const SimpleList& right);
            ~SimpleList();
        private:
            struct node {
                value_type data;
                node* next;
            };
            node* list;
    };
}
#endif



// Here is the file simplelist.cpp

#include <iostream>
#include "simplelist.h"
using namespace std;

namespace harden_list {
    SimpleList::SimpleList() {
        list = nullptr;
    }



    void SimpleList::insert(const value_type& insertMe) {
        node* temp = new node;
        temp -> data = insertMe;
        temp -> next = list;
        list = temp;
    }



    void SimpleList::print() const {
        node* tempPtr = list;
        while (tempPtr != nullptr) {
            cout << tempPtr -> data << " ";
            tempPtr = tempPtr -> next;
        }
    }


    SimpleList::size_type SimpleList::size() const {
        size_type count = 0;
        node* tempPtr = list;

        while (tempPtr != nullptr) {
            count++;
            tempPtr = tempPtr -> next;
        }

        return count;
    }


    SimpleList::value_type SimpleList::find(
                const value_type& findMe, 
                bool& found) const {

        node* curPtr = list;
        while (curPtr != nullptr && curPtr -> data != findMe) { 
            curPtr = curPtr -> next;
        }

        // assert: curPtr -> data == findMe || curPtr == nullptr

        if (curPtr != nullptr) {
            found = true;
            return curPtr -> data;
        } else {
            found = false;
            return value_type();
        }
    }


/* ALTERNATE VERSION OF FIND()

    SimpleList::value_type SimpleList::find(
                const value_type& findMe, 
                bool& found) const {
                    
        node* curPtr = list;
        while (curPtr != nullptr) {
            if (curPtr -> data == findMe) {
                found = true;
                return curPtr -> data;
            }
            curPtr = curPtr -> next;
        } 
        found = false;
        return value_type();
    }
*/




    void SimpleList::del(const value_type& deleteMe, bool& found) {
        node* prevPtr = list;

        if (list == nullptr) {
            found = false;
        } else if (list -> data == deleteMe) {
            node* tempPtr = list;
            list = list -> next;
            delete tempPtr;
            found = true;
        } else {
            while (prevPtr -> next != nullptr && prevPtr -> next -> data != deleteMe) { 
                prevPtr = prevPtr -> next;
            }

            if (prevPtr -> next == nullptr) {
                found = false;
            } else {
                node* tempPtr = prevPtr -> next;
                prevPtr -> next = prevPtr -> next -> next;
                delete tempPtr;
                found = true;
            }
        }
    }


    SimpleList::SimpleList(const SimpleList& copyMe) {
        clone(copyMe);
    }


    SimpleList SimpleList::operator=(const SimpleList& right) {
        if (this != &right) {
            clear();
            clone(right);
        }
        return *this;
    }


    SimpleList::~SimpleList() {
        clear();
    }



    void SimpleList::clear() {
        node* tempptr = list;
        while (tempptr != nullptr) {
            list = list -> next;
            delete tempptr;
            tempptr = list;
        }
    }



    // Note: This function looks really long, but most of it is the explanations that
    // I have added.  There are 13 lines of actual code.

    void SimpleList::clone(const SimpleList& copyMe) {
        if (copyMe.list == nullptr) {
            list = nullptr;
        } else {
        
            // 1. Copy the first node in the original list
            
            list = new node;
            list -> data = copyMe.list -> data;

            // 2. Get sourcePtr and newListPtr set up to copy the remaining nodes:
            // 2a. newListPtr should always point to the last node we created in the new list
            // 2b. sourcePtr should always point to the next node to be copied in the original list
                        
            node* newListPtr = list;
            node* sourcePtr = copyMe.list -> next;
            
            // 3. Now copy the rest of the list
            
            while (sourcePtr != nullptr) {
            
                // 3a. Add a new node to the end of the new list
                // 3b. Move newListPtr down to the newly added node (to meet rule 2a above)
                // 3c. Populate the newly added node
                // 3d. Advance sourcePtr to the next node to be copied in the original list
                //     (to meet rule 2b above)
                               
                newListPtr -> next = new node;
                newListPtr = newListPtr -> next;
                newListPtr -> data = sourcePtr -> data;
                sourcePtr = sourcePtr -> next;
            }
            
            // 4. Make sure the list ends with a nullptr
            
            newListPtr -> next = nullptr;
        }
    }
}

Section 20.7: The LL class

The STL has a container class named "list" that is implemented using linked lists. Next we will do an example that will be our own version of this class. (Technical note: actually what we will be implementing will be a version of the STL forward_list class. The STL list class is actually more complicated, since it allows traversing the list both forward and backward.)

Here's our client program to test the class we are going to write. Make sure you study it carefully so you understand what it is that we need our class to do.

#include <iostream>
#include "LL.h"
using namespace std;

void print(const LL<int>& printMe);


int main() {
    LL<int> l1, l2;
    
    l1.push_front(1000);
    LL<int>::iterator it = l1.begin();
    for (int i = 0; i < 10; i++) {
        l1.insert_after(it, i);
        l2.push_front(i);
    }

    cout << "l1: ";
    print(l1);
    
    cout << "l2: ";
    print(l2);
    
    cout << "Size of l1: " << l1.size() << endl;
    it = l1.begin();
    l1.delete_after(it);
    cout << "Setting iterator to first item in l1 and calling delete_after(): " 
         << endl;
    cout << "l1: ";
    print(l1);
    cout << "New size of l1: " << l1.size() << endl;
    
    l1.front() = 1001;
    cout << "Using front to set first item in l1 to 1001: ";
    cout << "l1: ";
    print(l1);
    
    cout << "Using front() to print first item in l1: " << l1.front() << endl;
    
    cout << "Using empty(), pop_front(), and front() to print l1 and "
         << "also clear it: " << endl;
    
    while (!l1.empty()) {
        cout << l1.front() << " ";
        l1.pop_front();
    }
    cout << endl;
    
    cout << "l1 should be empty, so testing Empty_List_Error on it: " << endl;
    try {
        l1.pop_front();
    } catch (LL<int>::Empty_List_Error e) {
        cout << "oops, tried to pop_front() from l1 but it was empty! " << endl;
    }
}    


void print(const LL<int>& printMe) {
    for (LL<int>::const_iterator i = printMe.begin(); i != printMe.end(); i++) {    
        cout << *i << " ";
    }
    cout << endl;
}

Now the header file and implementation file. Notice that there are two versions of the front() function. We'll see why in lesson 20.8

//  This is the file LL.h

#ifndef LL_h
#define LL_h

#include <cstdio>

template <class T>
class LL {
  public:
    typedef size_t size_type;
    typedef T value_type;

  private:
    struct node {
        value_type data;
        node* next;
    };
    node* list;


  public:
    class iterator {
      public:
        iterator(node* initial = nullptr) {
            current = initial;
        }
        
        value_type& operator*() const {
            return current->data;
        }

        iterator& operator++() {
            current = current->next;
            return *this;
        }

        iterator operator++(int) {
            iterator original(current);
            current = current->next;
            return original;
        }

        bool operator==(iterator other) const {
            return current == other.current;
        }

        bool operator !=(iterator other) const {
            return current != other.current;
        }
        
        const node* link() const {
            return current;
        }
        
        node*& link() {
            return current;
        }
        
      private:
        node* current;
    };
    
    
    class const_iterator  {
      public:
        const_iterator(const node* initial = nullptr) {
            current = initial;
        }

        const value_type& operator*() const {
            return current->data;
        }

        const_iterator& operator++() {
            current = current->next;
            return *this;
        }

        const_iterator operator++(int) {
            const_iterator original(current);
            current = current->next;
            return original;
        }

        bool operator==(const const_iterator other) const {
            return current == other.current;
        }

        bool operator !=(const const_iterator other) const {
            return current != other.current;
        }
        
        const node* link() const {
            return current;
        }
        
        node*& link() {
            return current;
        }
      private:
        const node* current;
    };  // end of iterator class declarations.  LL class continues below.

    iterator begin() {
        return iterator(list);
    }

    iterator end() {
        return iterator();
    }

    const_iterator begin() const {
        return const_iterator(list);
    }

    const_iterator end() const {
        return const_iterator();
    }

    class Empty_List_Error{};
    LL();
    LL(const LL& copyMe);
    LL operator=(const LL& right);
    ~LL();
    bool empty() const;
    size_type size() const;
    void clone(const LL& copyMe);
    void clear();
    void pop_front();
    void push_front(const value_type& item);
    value_type& front();
    const value_type& front() const;
    void insert_after(iterator& position, const value_type& insertMe);
    void delete_after(iterator& position);
};


#include "LL.cpp"
#endif



//  This is the file LL.cpp

#include <cassert>
#include <iostream>
using namespace std;

template <class T>
LL<T>::LL () {
    list = nullptr;
}

template <class T>
void LL<T>::delete_after(iterator& position) {
    assert (position.link() -> next != nullptr);    
    node* tempptr = position.link() -> next;
    position.link() -> next = position.link() -> next -> next;
    delete tempptr;
}



template <class T>
void LL<T>::insert_after(iterator& position, const value_type& insertMe) {
    node* newnode = new node;
    newnode -> data = insertMe;
    newnode -> next = position.link() -> next;
    position.link() -> next = newnode;
    position.link() = newnode;
}



template <class T>
void LL<T>::pop_front() {
    if (empty()) {
        throw Empty_List_Error();
    } else {
        node* deleteMe = list;
        list = list->next;
        delete deleteMe;
    }
    
}





template <class T>
typename LL<T>::value_type& LL<T>::front() {
    if (empty()) {
        throw Empty_List_Error();
    } else {
        return list->data;
    }
}





template <class T>
const typename LL<T>::value_type& LL<T>::front()  const {
    if (empty()) {
        throw Empty_List_Error();
    } else {
        return list->data;
    }
}






template <class T>
void LL<T>::clear() {
    node* deleteMe;
    while (list != nullptr) {
        deleteMe = list;
        list = list->next;
        delete deleteMe;
    }
}





// Note this is an exact copy of the clone() function from SimpleList

template <class T>
void LL<T>::clone(const LL<T>& copyMe) {
    if (copyMe.list == nullptr) {
        list = nullptr;
    } else {        
        list = new node;
        list -> data = copyMe.list -> data;

        node* newListPtr = list;
        node* sourcePtr = copyMe.list -> next;        
        while (sourcePtr != nullptr) {
            newListPtr -> next = new node;
            newListPtr = newListPtr -> next;
            newListPtr -> data = sourcePtr -> data;
            sourcePtr = sourcePtr -> next;
        }
        
        newListPtr -> next = nullptr;
    }
}





// returns the number of items in the LL object.
template <class T>
typename LL<T>::size_type LL<T>::size() const {
    LL<T>::size_type numberOfItems = 0;
    node* curPtr = list;
    while (curPtr != nullptr) {
        ++numberOfItems;
        curPtr = curPtr->next;
    }
    return numberOfItems;
}





// returns true if the LL object is empty, false otherwise.
template <class T>
bool LL<T>::empty() const {
    return list == nullptr;
}





// insert x at the front of the LL object.
template <class T>
void LL<T>::push_front(const value_type& item) {
    node* oldList = list;
    list = new node;
    list->next = oldList;
    list->data = item;
}











// THE BIG-3

template <class T>
LL<T>  LL<T>::operator=(const LL<T> & right) {
    if (this != &right) {
        clear();
        clone(right);
    }
    return *this;
}





template <class T>
LL<T>::LL (const LL<T> & copyMe) {
    clone(copyMe);
}






template <class T>
LL<T>::~LL() {
    clear();
}

Section 20.8: Two versions of "front()"

Let's look at the "front()" member function. It returns the first item in an SimpleList object. We would like to be able to use this function in the usual way -- for example, "cout << list1.front();". But we'd also like this function call to be allowed on the left side of an assignment operator, so that we can use it to modify the first item in an SimpleList object -- for example, "list1.front() = 47;". (The STL "list" class has a member function named "front()" that behaves this way.) This will require us to have two versions of the front() function. In order to understand why we need two versions, consider the following client.

#include <iostream>
#include <cassert>
#include "ll.h"
using namespace std;
using namespace cs_linkedlist;

int main() {

// part 1

     LL l1;
     l1.push_front(1);
     cout << "cout << l1.front(); should be 1: ";
     cout << l1.front() << endl;
     
     
     
 // part 2
 
     l1.front() = 2;
     cout << "cout << l1.front(); should be 2: ";
     cout << l1.front() << endl;     
     
     
     
// part 3

     const LL l2(l1);
     cout << "cout << l2.front(), should be 2: ";
     cout << l2.front() << endl;

     
 // part 4
 
     l2.front() = 2;
     cout << "cout << l2.front(), should cause error: ";
     cout << l2.front() << endl;
}

Here is an explanation of why we cannot solve this problem with just one version of the front() function. We must have two version.

First note that the difference will be only in the function header. The bodies of these two functions will be identical.

Parts 1, 2, and 3 in the LL example above should work. Part 4 should give a syntax error. Make sure this makes sense before reading on.

1. If we only have the basic form, int front(), then we can't have front() on the left of an assignment operator (i.e., we want part 2 to work, but it will give a syntax error).
2. If we change it to int& front(), then front() cannot be called with a const LL calling object (i.e., we want part 3 to work, but it will give a syntax error).
3. If we change it to int& front() const, then a const LL calling object is allowed on the left side of an assignment operator (i.e., part 4 works, but should not).

The solution is to have 2 versions of front():

   int front() const;
   int& front();

One additional complication: Because we expect that we will be making this into a templated class, the return type may be an object. So, just like we pass parameters that are objects by const-reference instead of by value, we change the return type of our front() function from "return-by-value" to "return by const-reference". So, the final form will be:

   
   const int& front() const;
   int& front();