CIS 255 (CS1) Programming Methods: Java
Lesson 22: Recursion
Note: I converted this from my C++ based introduction to recursion. Please let me know if you find anything left over from C++ that I failed to convert.
Section 22.1: Introduction to Recursion
Up to now whenever we have needed to repeat actions in a program we have used some kind of a loop. This technique is called "iteration". A second technique for causing actions in a program to repeat is called recursion. Recursion happens when a method calls itself. (Technical note: you could also have recursion if you have two methods that call each other. We will not discuss this technique in this class.)
Before we delve into recursion there are four preliminary observations I would like to make.
First, you should only write a method that calls itself when you specifically want to use recursion and you understand what you are doing. I have had students submit assignments in which they had a method calling itself only because they didn't understand how to use a loop to handle the repetition. Using recursion in this manner is really bad practice.
Second, it is important to realize that you can always use iteration to write any program. In other words, recursion is a programming tool that can simplify your code (in some cases dramatically) but is never required. Any program that you write using recursion could be rewritten using iteration. Not necessarily easily, but it could be done. The reverse is also true: any program written using iteration could be rewritten using recursion.
Third, there are always two ways of looking at a recursive solution to a problem. One is what I like to call the "leap of faith" method. As you will soon see, when writing a recursive method we are allowed to assume (with certain restrictions) that the method we are writing already exists and works as desired. Although this is mathematically provable (don't worry, we won't go there), it is difficult for many students to feel comfortable with. You will find recursion to be much easier to use if you can get yourself to take this "leap of faith".
The second way to look at a recursive solution to a problem is to try to follow through with each recursive method call, looking at the processes in precise detail, to understand what is really going on in the computer when the method is executed. We will see that this can get you buried in details rather quickly. Although we will discuss some techniques for getting to the details like this, it is highly recommended that you avoid this as much as possible when writing your recursive methods. Keeping things at the "leap of faith" level will usually serve our needs much better.
Fourth, often when writing a recursive method it is hard to see how things are going to fit together when you start. The best strategy is to follow the steps I will outline below, gradually building up and filling in the pieces of the recursive method, and (hopefully) before you know it the entire method will be done.
Section 22.2: The pow Method
In order to explain the process of writing a recursive method let's use a simple example. We will write a power() method that performs exponentiation. To keep things simple, we will require the base to be an integer and the exponent to be a non-negative integer. Here is the header for our power method:
int power(int base, int exponent)
The first question to ask yourself when writing a recursive method is "what is the base case?" The base case is used to make sure that the recursive method does not recurse infinitely. If the method calls itself every time it is called, then it will never stop. So there must be a situation in which the method does NOT call itself. To get more specific, the base case for a problem should be a case of the problem that can be solved immediately without having to call the method again. Furthermore, it should be the simplest such case. For example, in our power method, the base case could be exponent == 2, because when the exponent is 2 we can immediately return base * base as the return value of the method. However, the case where exponent == 1 is simpler and so is preferable. In fact, there is a simpler case yet: when exponent == 0, we can immediately return 1 as the return value of the method (since anything raised to the 0 power is 1).
Having determined the base case, we can now write part of our method:
public static int power(int base, int exponent)
{
if (exponent == 0){
return 1;
} else {
[to be continued...]
}
}
See? We are already half way through writing our method! Now on to the second question: what do we want to do in the recursive case? There are several hints that we can use to figure out how to proceed. (1) this is a value-returning method, so each case, including the recursive case, is probably going to involve a return. (2) Since this is a recursive method, we know that there is going to be a call to power somewhere in the return statement. (3) An important rule (perhaps the most important rule) for writing recursive methods is that when you make the recursive call you must use an argument that gets you closer to the base case. If you do this, then you can assume that the method call does what it is supposed to do, even though you haven't finished writing the method yet (this is the leap of faith I mentioned above). In our case, the base case checks to see if exponent is 0, so the argument in our recursive call will have to be something smaller than the current value of exponent. A good first try is to simply subtract 1 from exponent to make it smaller. Putting these observations together, we have
public static int power(int base, int exponent)
{
if (exponent == 0){
return 1;
} else {
return ... power(base, exponent - 1);
}
}
The only thing left for us to do is to figure out what should go in the place of the ... in the code above. We use the fact that Xn is equal to X times Xn - 1 to determine that we need to multiply our method call by base in order to return the correct answer. Here is the final result, which has been placed in a complete C++ program:
class Power {
public static void main(String[] args)
{
int result;
result = power(2, 3);
System.out.println(result);
}
public static int power(int base, int exponent)
{
if (exponent == 0){
return 1;
} else {
return base * power(base, exponent - 1);
}
}
}
Section 22.3: Analyzing the power Method -- Technique #1
Now we are going to use two different techniques to take a close look at the details behind how this recursive method works. The first technique is a good way to predict the results of a recursive method call. You might want to use this technique if you are writing a recursive method and you aren't getting the results you expect. This technique also might come in handy if you are doing your exercises or taking the final and you are asked to predict the results of a recursive method call.
The technique involves making a table with three columns. In the left column we will write our method call. In the middle column we will write the intermediate result of this method call. It is called an "intermediate result" because with a recursive method call we can't immediately determine the final result. This intermediate result will likely involve a call to the same method with arguments that are closer to the base case of the method. In the third column of our table we will write the final result. As you will see, the first and second column will be filled as we go down the table, and then the third column will be filled as we go back up the table, with the final result of the original method call finally appearing at the top of the third column.
Let's take a look at what happens when we call our power method with arguments 2 and 3. Here is the initial setup of our table:

Looking at the code of our power method, we see that, because exponent is not equal to 0, the intermediate result of the method call is base * power(base, exponent -1) or, in our case, 2 * power(2, 2). Let's add this to our table:

We are now faced with the problem that we don't know what power(2, 2) is. So we start a new row in our table, placing power(2, 2) in the first column because that is now what we need to compute:

Continuing in this way we eventually end up with power(2, 0) in the left column. Looking at our code again, we see that the intermediate result for this method call is "1":

We have finally reached a point where we can actually write in the final result, since the intermediate result doesn't include any method calls:

Now that we have a final result, we can start working our way back up the table. The fourth row in our table tells us that power(2, 0) has a final result of "1", so we can now compute the final result in the third row: 2 * power(2, 0) == 2 * 1 == 2:

Continuing on up the table in this way we can complete the second row of the table and then the first row of the table:

This tells us that the result of the original method call is 8.
This is a good technique for determining the result of a recursive method call. Note that in other cases (for example if the method is not a value-returning method but produces some output) you may have to be creative to get this technique to work, but it has never failed me. I hope that seeing the recursive calls play out as you have seen in this example helps you to understand what is going on behind the scenes when you call a recursive method.
Section 22.4: Analyzing the power Method -- Technique #2
Let's now analyze the power method using a second technique. This technique is more complex than the last one, so you probably won't want to use it in your own analyses of recursive methods. I show it here only to give you a better understanding of how the computer itself actually handles a call to a recursive method. I suggest that you follow the explanation carefully, despite its tediousness.
All local variables are stored in a highly structured part of memory called the stack. Each time a method is called, all of the memory that that method will need is allocated on the stack in what is called an activation record for that method call. The first activation record on the stack will always be an activation record for the method main. Our main method (see the complete program listed in section 1 above) has one local variable, result, so this first activation record will have to include memory for that variable. In addition (this is a complex but important point!), whenever a method calls a value returning method, its activation record will need some place to store the value that gets returned. In our pictures we will label this memory location with the abbreviation "ret" (short for "returned value"). So here is a picture of the stack with the initial activation record for main:

Now let's start executing the statements inside main. The first thing that happens is the method power is called, so we need to add an activation record for this method call. This activation record will include 2 memory locations for the two parameters, an additional memory location to store the return value of the method call that appears in the method, and one additional thing: the computer will have to have some way of knowing where to return to when this method is done executing. In other words, we need to know which of the calls to the power method that we see in our program initiated this activation record. The computer does this by storing in this activation record the memory address of the next machine instruction to be executed when the execution of this method ends. To simplify things, we will number the calls to power: the call from main will be call #1, and the call from inside power will be call #2. Then we just have to store either 1 or 2. Since the initial call to power is from main, we will store a 1 in a memory location named "called from" as pictured here:
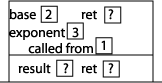
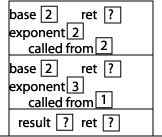
Now we can start executing the statements inside power. Since exponent is not equal to 0, we execute the "else" part of the if statement, which involves a method call to the method power, this time with arguments 2 and 2. We put a "2" in the called from memory location to indicate that the method was called from within power. Setting up that activation record results in this picture of the stack:
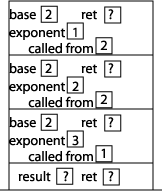
Now we can start executing the statements inside power. Since exponent is not equal to 0, we execute the "else" part of the if statement, which involves a method call to the method power, this time with arguments 2 and 1. We put a "2" in the called from memory location to indicate that the method was called from within power. Setting up that activation record results in this picture of the stack:
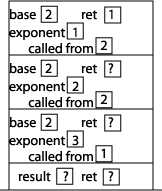
Now we can start executing the statements inside power. Since exponent is not equal to 0, we execute the "else" part of the if statement, which involves a method call to the method power, this time with arguments 2 and 0. We put a "2" in the called from memory location to indicate that the method was called from within power. Setting up that activation record results in this picture of the stack:

Now we can start executing the statements inside power. Since exponent is now equal to 0, we execute the "if" part of the if statement. We execute the "return 1" statement by placing a 1 in the "ret" memory address of the previous activation record. Since the current power method is now done executing, we check the value stored in the "called from" memory address, which tells us to continue execution from the method call to power inside power. In addition, we erase the current activation record from the stack:
Continuing our execution, we find that we are in the middle of executing the statement "return base * power(base, exponent - 1);". The value of "power(2, 0)" (stored in the "ret" memory location) is 1, so we want to return 2 * 1 which is 2. This result gets stored in the "ret" memory location of the previous activation record. Since the current power method is now done executing, we check the value stored in the "called from" memory address, which tells us to continue execution from the method call to power inside power. In addition, we erase the current activation record from the stack:
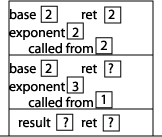
Continuing our execution, we find that we are in the middle of executing the statement "return base * power(base, exponent - 1);". The value of "power(2, 1)" (stored in the "ret" memory location) is 2, so we want to return 2 * 2 which is 4. This result gets stored in the "ret" memory location of the previous activation record. Since the current power method is now done executing, we check the value stored in the "called from" memory address, which tells us to continue execution from the method call to power inside power. In addition, we erase the current activation record from the stack:
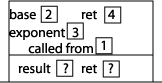
Continuing our execution, we find that we are in the middle of executing the statement "return base * power(base, exponent - 1);". The value of "power(2, 2)" (stored in the "ret" memory location) is 4, so we want to return 2 * 4 which is 8. This result gets stored in the "ret" memory location of the previous activation record. Since the current power method is now done executing, we check the value stored in the "called from" memory address, which tells us to continue execution from the method call to power inside main. In addition, we erase the current activation record from the stack:

Continuing our execution (back in main now), we find that we are in the middle of executing the statement "result = power(2, 3);". The value of "power(2, 3)" (stored in the "ret" memory location) is 8, so we want to assign result the value 8, which then is output by the cout statement.
Section 22.5: The findSmallest Method
In the rest of this lesson we will basically be developing a series of increasingly complex recursive methods. I strongly suggest that you spend a few minutes trying to write each of these methods on your own before reading the solution. In each section I will present a problem, give a method header for the method we are going to write, and then suggest that you stop reading and try it on your own.
The first method we will attempt will be named "findSmallest". This method will take one argument that is an array of integers and a second argument that is an int that indicates how many elements of the array are being used (i.e. how many items are in the array). The method should return the smallest item in the list. Here is our method header:
public static int findSmallest(int[] list, int numItems)
Now is where you should stop reading and try this on your own!
What should our base case be? Ask yourself: what is a situation in which we can easily determine result of the method without making a recursive call? When the number of items in the list is 1! When numItems == 1, that single item is the smallest item, and so we simply return it.
It is a good idea to always ask yourself after you have thought of a base case if there is a simpler base case. In this case, we might wonder whether a simpler base case would be when the number of items in the list is 0. But what should this method return if the number of items in the list is 0? It doesn't really make sense to call this method when the number of items is 0. So we need to impose a pre-condition for this method: numItems > 0.
Here is our code so far:
public static int findSmallest(int[] list, int numItems)
{
if (numItems == 1){
return list[0];
} else {
[to be continued...]
}
}
Now for our recursive case. Remember that when trying to write the recursive case, we can call the method we are writing as long as we call it with arguments that get us closer to the base case. What might that method call look like? Since the base case occurs when numItems == 1, it makes sense that we would call it with numItems reduced by 1:
findSmallest(list, numItems - 1);
What will this method call give us? The smallest item in the list not counting the last item! Can we use this information to figure out what the smallest item in the entire list is? Yes. If the last item in the list is smaller than the result of this method call, then we should return the last item in the list. Otherwise, we should return the result of this method call. Translating that last sentence into C++ we get the following method:
public static int findSmallest(const int list[], int numItems)
{
if (numItems == 1){
return list[0];
} else if (list[numItems - 1] < findSmallest(list, numItems - 1)){
return list[numItems - 1];
} else {
return findSmallest(list, numItems - 1);
}
}
This method will work, but there is some ugliness to it. In a recursive method, making recursive calls multiple times is extremely inefficient, because each of those recursive calls may result in a large number of additional method calls. If we can avoid this we should, and in this case there is no reason to calculate the smallest item in the list twice. Let's just do it once and store the result in a local variable:
public static int findSmallest(int[] list, int numItems)
{
if (numItems == 1){
return list[0];
} else {
int smallest = findSmallest(list, numItems - 1);
if (list[numItems - 1] < smallest){
return list[numItems - 1];
} else {
return smallest;
}
}
}
(*Technical note: to be clear, it is fine to have multiple recursive method calls in your method if only one of them is called each time through the method. The problem is when a single time through the method results in multiple recursive method calls. If this is confusing...don't worry too much about it, it is a minor point.)
This is better, but we can do even better if we take advantage of Java's min() method, which returns the smallest of its two arguments. Here is a complete program that we can use to test the final version of our findSmallest method:
import java.lang.*;
class FindSmallest {
public static void main(String[] args)
{
int[] list = {4,6,2,9,5,1,7,3};
int size = 8;
System.out.println("The smallest item in the list is "
+ findSmallest(list, size));
}
public static int findSmallest(int[] list, int numItems)
{
if (numItems == 1){
return list[0];
} else {
return Math.min(list[numItems - 1],
findSmallest(list, numItems - 1));
}
}
}Section 22.6: The printVertical Method
We will now write a method called printVertical that will take a single integer argument and write the integer vertically, one digit per line. We will assume that the argument is non-negative. So, for example, if we call the method like this:
printVertical(9746);
We should get the following output:
97
4
6
This is an appropriate example for us to work on at this point because we have not yet done a recursive method that is void and that produces output. Things may look a little different, but the rules for writing recursive methods outlined so far in this lesson still apply.
You might think for a moment about how you would do this without using recursion. It is possible, but not easy. (If you don't think it would be all that hard, take a few moments and write it!) Here is our method header:
public static void printVertical(int num)
Now is where you should stop reading and try this on your own!
What should our base case be? If num has only one digit, then we can just print out the number and be done with it. How can we check to see that it has only one digit? Just check to see if it is less than 10. Here is our code so far:
public static void printVertical(int num)
{
if (num < 10){
System.out.println(num);
} else {
[to be continued...]
}
}
What do we want to do in the recursive case? When writing a recursive method, if the recursive call is not immediately obvious to you, ask yourself: How should I call the method recursively so that (1) the arguments get me closer to the base case and (2) the method call helps me get to the solution to the problem. In the case of printVertical, my first thought might be to subtract 1 from num for my recursive call, since that gets me closer to the base case of num < 10. However, calling printVertical with num - 1 as the argument doesn't really help me with the problem of printing num vertically. For example, if num is 9746, printing the number 9745 vertically doesn't really help me. What would help me? What if I could print the number 974 vertically? That would help! Then I would just have to print the digit 6 and I'd be done! Can I call printVertical and have it print everything except the last digit? Yes. Call it with an argument of num / 10. 9746 / 10 is 974! So the solution is to call printVertical with an argument of num / 10 to print all of the digits except for the last one, and then print the last digit by printing the expression num % 10. Here is our complete code, including a driver program:
class PrintVertical {
public static void main(String[] args)
{
printVertical(9746);
}
public static void printVertical(int num)
{
if (num < 10){
System.out.println(num);
} else {
printVertical(num / 10);
System.out.println(num % 10);
}
}
}Section 22.7: Towers of Hanoi
In the mountains near the city of Hanoi there is a Buddhist monastery. Outside the monastery there are three tall towers (which we will call LEFT, MIDDLE, and RIGHT) and 64 stone disks. Each of the disks has a hole in its center so that it can be placed on one of the towers (think of the towers as poles). Each disk is a different size. At the beginning of time, all 64 disks were stacked on the LEFT tower, ordered from largest (on the bottom) to smallest (at the top). Day and night the monks who live in the monastery unceasingly move disks one at a time from one tower to another. They never place a disk on a tower that holds a smaller disk. When they have moved all 64 disks from the LEFT tower to the RIGHT tower, it will be the end of time.
I don't know about you, but this has me a bit worried, so I've decided to write a method to simulate this process, and then analyze the method to see how much time I have left.
I suggest that you run a Towers of Hanoi simulation a few times to become familiar with the problem.
If we play with this problem for awhile we begin to see a pattern in the solutions. For example, when we move 4 disks from the LEFT tower to the RIGHT tower, we always begin by using a sequence of moves to get 3 disks from the LEFT tower to the MIDDLE tower; then we move the 1 remaining disk from the LEFT tower to the RIGHT tower; finally we use a sequence of moves to get those 3 disks that are sitting on the MIDDLE tower to the RIGHT tower. Let's state this more generally. Assume that there are n disks on the LEFT tower. The problem can be solved by moving n - 1 disks from the LEFT tower to the MIDDLE tower, then moving the remaining disk on the LEFT tower to the RIGHT tower, then moving the n - 1 disks that are sitting on the MIDDLE tower to the RIGHT tower. By now I hope that this sounds to you like a naturally recursive method. We can move the n - 1 disks by using a recursive call.
Let's write our recursive method now. Rather than use fancy graphics, we will write a method that prints out instructions for solving the problem. For example, here is the output that our method should produce if the number of disks is 4:
move a disk from the LEFT tower to the MIDDLE tower. move a disk from the LEFT tower to the RIGHT tower. move a disk from the MIDDLE tower to the RIGHT tower. move a disk from the LEFT tower to the MIDDLE tower. move a disk from the RIGHT tower to the LEFT tower. move a disk from the RIGHT tower to the MIDDLE tower. move a disk from the LEFT tower to the MIDDLE tower. move a disk from the LEFT tower to the RIGHT tower. move a disk from the MIDDLE tower to the RIGHT tower. move a disk from the MIDDLE tower to the LEFT tower. move a disk from the RIGHT tower to the LEFT tower. move a disk from the MIDDLE tower to the RIGHT tower. move a disk from the LEFT tower to the MIDDLE tower. move a disk from the LEFT tower to the RIGHT tower. move a disk from the MIDDLE tower to the RIGHT tower.
Let's first think about what our parameters will need to be. We'll need to know how many disks to move, which tower we are moving the disks from (the source), which tower we are moving the disks to (the target), and which tower we are using for temporary storage (the storage). Here is the method header:
public static void moveDisks(int numDisks,
String source,
String target,
String storage)
A method call that would result in the output given above would be:
moveDisks(4, "LEFT", "RIGHT", "MIDDLE");Now is where you should stop reading and try this on your own!
What should the base case be? We could choose numDisks == 1 for our base case, but there is a simpler base case. We'll go with numDisks == 0. What action do we take if numDisks is 0? None! So one way to structure our solution would be
public static void moveDisks(int numDisks,
String source,
String target,
String storage)
{
if (numDisks == 0){
; // do nothing!
} else {
[to be continued...]
}
}
This, however, is a little clumsy. Let's reverse the condition in the if statement so that we have an if with no else. This will look a little different from the typical recursive method in which you can explicitly see both the base case and the recursive case, but it will be better code. You'll just have to remember that the base case is there implicitly because the method does nothing if the if condition is false. Here is our improved way to structure the solution:
public static void moveDisks(int numDisks,
string source,
string target,
string storage)
{
if (numDisks > 0){
[recursive case]
}
}
What do we want to do in the recursive case? This is where the strategy described above comes into play. We will first use a recursive call to move numDisks - 1 disks from the source to the storage (note that the argument in the recursive call will be numDisks - 1, which means we'll be getting closer to our base case of numDisks == 0). Then we will use a cout statement to print the instruction to move one disk from the source to the the target. Finally we will use a second recursive call to move those numDisks - 1 disks that are sitting on the storage tower to the target. Here is our final program, which will produce the output shown above.
class Towers {
public static final int NUM_DISKS = 4;
public static void main(String[] args)
{
moveDisks(NUM_DISKS, "LEFT", "RIGHT", "MIDDLE");
}
public static void moveDisks(int numDisks,
String source,
String target,
String storage)
{
if (numDisks > 0){
moveDisks(numDisks - 1, source, storage, target);
System.out.println("move a disk from the " + source
+ " tower to the " + target + " tower.");
moveDisks(numDisks - 1, storage, target, source);
}
}
}
In case you are having trouble understanding how the different names for the towers are working together in this method, here is an explanation: When you call moveDisks, the first tower that you list as an argument is always where the disks are being moved from, the second tower that you list is always where the disks are being moved to, and the third tower that you list is always the remaining tower (that can be used for storage if needed).
So, for example,
moveDisks(numDisks - 1, source, storage, target);
means "move disks from the source tower to the storage tower, using the target tower as temporary storage."
Section 22.8: Analyzing Towers of Hanoi
I hope you can read this section slowly enough to really enjoy it. I think it is a lot of fun.
I still want to find out how long I have to enjoy before the end of time hits. Let's figure out how long it will take those monks to move the 64 disks from the LEFT tower to the RIGHT tower. Let's start by figuring out how many moves it will take. 1 disk takes 1 move. 2 disks take 3 moves. 3 disks take 7 moves. How many moves will 4 disks take? Can I calculate this without actually counting? Sure. To move 4 disks we first move 3 disks (7 moves), then we move 1 disk (1 move), then we move 3 disks again (7 moves) for a total of 15 moves. Using the same technique, we find that 5 disks take 31 moves (15 + 1 + 15) and 6 disks take 63 moves (31 + 1 + 31). Let's try to find a formula that tells us how many moves it takes to move n disks. Here's a table listing our results so far:
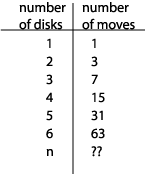
The key to finding a formula for moving n disks is to notice that you can get each of the numbers in the right column of this table by taking 2 raised to the power of the corresponding number in the left column and then subtracting 1. In other words, if the number of disks is n, the number of moves required is 2n - 1.
Where does this leave us? The number of moves required to move 64 disks is 264 - 1, which is about 1.8 X 1019. So how much time will this take? Let's assume that the monks can move 1 disk per minute. (I think this is a lot faster than the monks can actually move the disks, since those stone disks are quite heavy, but let's go with this estimate and see what happens.) Based on this assumption, it will take the monks 1.8 X 1019 minutes to move the disks. Dividing this by 60 to find out how many hours it will take them gives us about 3 X 1017 hours. Dividing by 24 to find out how many days gives us about 1.3 X 1016 days. Dividing by 365 to find out how many years gives us about 3.5 X 1013 (about 35 trillion) years. Whew, I'm feeling much better now.
Just for fun, let's talk about how long it would take a computer to move the disks. To give the computer an advantage, let's take out the cout statement so that the instructions don't actually have to be output, just calculated internally. When I did this on my computer with 23 disks it took about 12 seconds. Since it takes about 8,400,000 moves to move 23 disks, I figure that my computer is moving 700,000 disks per second (8,400,000 / 12). (Incidentally, I'm working on a 550Mhz Mac. When I tried this on a 500Mhz PC it came out to about 100,000 moves per second. And yes, this was done a long time ago :) 1.8 X 1019 moves. Dividing by 700,000 to find out how many seconds it would take my computer to move 64 disks we get 2.6 X 1013 seconds. Dividing by 60 to find out how many minutes gives us 4.4 X 1011 minutes. Dividing by 60 to find out how many hours gives us 7.3 X 109 hours. Dividing by 24 to find out how many days gives us 3 X 108 days. Dividing by 365 to find out how many years gives us 835,632 years. Still a pretty long time.
Part of the point of this analysis is to give you some experience with a problem that would take even a computer a very long time to solve. In a few applications worrying about a millisecond here and there is important, but in most applications other concerns far outweigh the concern of losing a millisecond or so. Where we start worrying about efficiency is when we get to some algorithms that could potentially take a completely unacceptable amount of time to run. In the case of the Towers of Hanoi problem, there does not seem to be a more efficient way to solve the problem; however, there are some unacceptably inefficient algorithms for which we have alternatives that are much faster.